“Unrolling” line charts are everywhere - where the lines gradually enter from origin, point by point. This is the world’s favourite way of animating a line chart, particularly as it makes a ton of sense when graphing a time series. d3 tends to transition line charts really weirdly, though. So what is d3 actually doing when creating transitions on line charts, and how can we make them prettier?
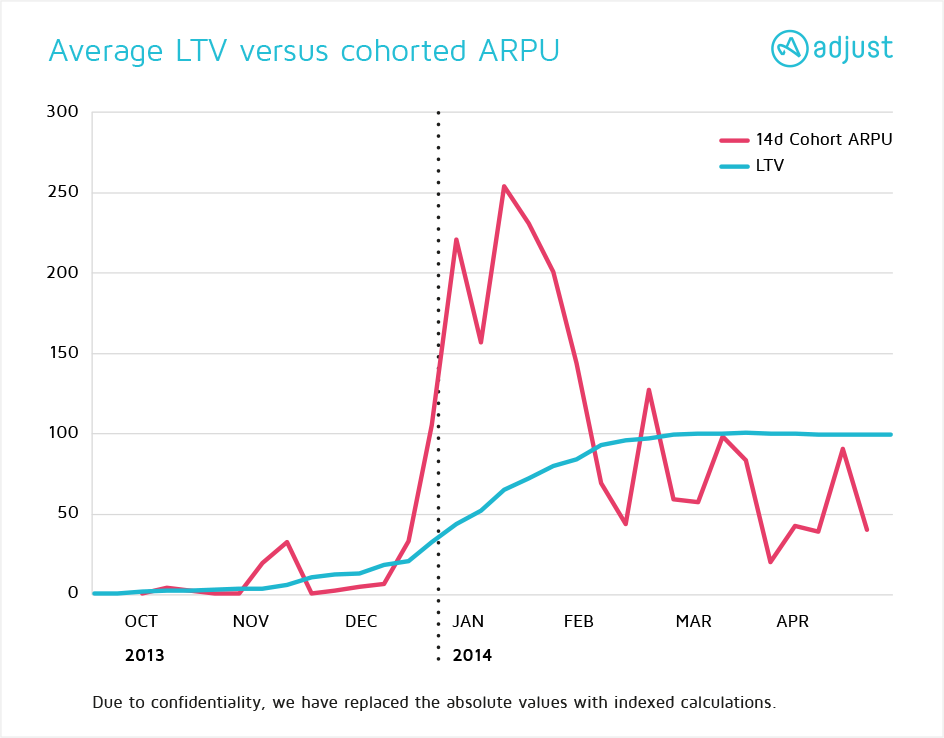
In the graph below, I had two series comparing two alternative calculations of lifetime value in mobile users. This was for a blog post, which we published here. The original version, as drafted by our talented designer, simply had two different graphs displayed at different points in the text - but I wanted to jazz it up a bit.
How SVG and d3 work with lines
Before we dig into generating transitions, you need to understand how the SVG standard and d3 interact when it comes to lines. SVG draws lines (more correctly, paths) from the points in a line being concatenated in a string, like this:
1
|
|
Normally, though, your data will be organized in a series of x: , y: datapoints, as an array of objects. d3 provides handy generators that take such arrays of objects, apply some transformation and scaling, and spit out the SVG string. Very easy:
1 2 3 4 5 6 7 8 |
|
In the problem above, where the second timeseries should be entered via a transition, we’ll start out with a line object with zero associated datapoints, i.e. an empty d string. Then we’ll ask d3 to .transition() to .attr('d', lineFunction(secondSeries). That’s the same pattern as we would use with any other transitions, except it looks awful:
N.B.: For code examples from here on, I’ll provide excerpts highlighting the method. For each step of the process, hit up the source code - JS in full is below each graph.
1 2 3 4 |
|
This isn’t what I was looking for at all! All the points simply spark into existence like some hitchhiker’s whale; that’s hardly a transition. d3, however, thinks it’s being entirely reasonable about this.
Whenever you create a transition in d3, you pass two states to d3: the initial state and the final state. You then ask d3 to interpolate between the two for each frame of the animation, expressed as a variable t {0,1}. In this example, you’re passing an empty string as the initial state, and a fully-generated string as the end state.
Because these are strings, d3 attempts to use interpolateString. This interpolation function runs a regex across the strings looking for numbers to manipulate. Except in this case, it finds no numbers in the initial state, and so manipulates nothing over t.
Ah-ha, you say, I’ll just pass the initial state as a string of origin coordinates! Yeah, no, I tried that:
1 2 3 4 5 6 7 8 |
|
As you see, d3 then finds all the (0,0) coordinates, then slowly scales them up to your end state coordinates, meaning that the line just appears in the top left of the graph and slowly scales into place. Matt Bostock discusses this himself and suggests some solutions for graphing realtime data here. All that said, this is still not unrolling properly.
The solution
For very simple graphs, you could simply clip or mask the path, and then move the mask over to the right as the animation progresses. That won’t be very scalable, though, as the complexity of the mask grows if you have multiple lines in the graph, or god forbid a background axis, as we do here. Besides, I find it a bit hacky. ;)
For a general solution, you need to tell d3 exactly how to interpolate between the two states using a custom interpolation function. Nick Rabinowitz posted a base interpolator here, which gives us the fundamental animation:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
What we’re doing here is creating a custom function, which returns the interpolation function, and passing a reference to that function to the attrTween of the transition. Transitions in d3 are created in several stages, where the transition is evaluated asynchronously. d3 calls the getInterpolation function once the transition is ready to go, and then evaluates the interpolation function that was returned for every frame t.
In this interpolation, for each t, we returned the d coordinate string, cropped to the latest whole datapoint for that particular t. d3 will figure out the steps of t required and call the function returned by getInterpolation for every frame in turn, and we will return the value of the line function for that subset. In large datasets, with maybe a few hundred datapoints, each or every other frame will add another point, so it’ll look perfectly smooth. With our smaller dataset, though, it looks rather choppy.
Let’s expand a little on Nick’s code to create a smoother, more general approach.
Fixing for a small dataset
So what we want to do now is smooth the animation out, giving not just the full datapoints for certain states, but also giving intermediary points for the t that don’t map to a full new point. For each t, we’ll pass the line function the sliced array with all the points that should be fully drawn, as well as a last intermediary point which has coordinates mapping to the middle state between the two points.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
|
This point needs a set of coordinates, x: , y:. x is easy: for each t, we’ll just pass the interpolated t value, which we know to be the current value between 0 and the end of the line. (To do this, we’ll swap out the quantile scale for a linear scale, and floor the scaled t when slicing the array.)
For y, we’ll calculate a weighted average of the current point and the next point. The weight would be the distance between x and x-1, which we can get by pulling the decimals of t:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
|
Now that’s looking pretty nifty. You’d probably not be surprised to learn that d3 already provides this kind of interpolation - in terms of interpolateObject and interpolateArray. Implementing these, however, turned out to be more code only to hack in the formats it expects, whereas we can more easily and readably simply provide the calculation of the average ourselves.
Fixing for arbitrary datasets
There’s one glaring flaw here, though, in that the interpolation function gleefully pulls a global variable for the data, instead of letting us define that on a transition-by-transition basis. If we had several arbitrary series to animate, letting that remain would mean declaring an entirely new, but identical function merely to use a different dataset, or constantly redefining the global dataset. That’s very silly.
It gets a bit muddy because d3 expects the interpolation function to pass a reference to a function which returns the interpolation function, so that the interpolation function can be fetched when the transition is started. That is, we need a reference to function getInterpolation to return a reference to function interpolate, which in turn calls function lineFunction.
To programmatically define the dataset we need, we need to wrap the, let’s say, function generator as an anonymous function in a return statement, and give the array as a parameter to a getGetInterpolation function:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
|
Using this, we can call the getInterpolation function with our series as a parameter, have that function evaluate to a reference of the function that returns a reference to interpolation, and use it seamlessly within standard d3 transitions.
Fixing for partial transition
Finally, in some cases we may already have part of the series displayed, and simply want to expand it to the right with the same animation. For example, imagine that we are displaying a metric over time, and that we then increase the timespan displayed. So we need to interpolate t to map to a certain subset of the series.
You may already have spotted that the interpolation functions are always provided with three arguments: function (d,i,a), where the d parameter is set to the current datum. With line graphs it’s often not necessary to bind the data to the elements, but in this case we want to access the data later.
With .datum() we can associate any data with the selected object, and thus receive it back in the interpolation function as the d parameter. We’ll simply set the scale range as starting at the end of the current dataset, and going to the end:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
|
Voilà. There’s plenty of ways we can expand upon this last exercise, for example by animating the scale as well, or by adding logic to allow for going backwards in the time series. The speed of the animation is also not even across the line, rendering more pixels per frame in certain segments, which makes it look like we are emphasising the portions of the line with higher delta; you could change the interpolate scale to scale t evenly on the number of pixels rendered.
That’s for another day, though.

